摘 要：為了克服常規PID穩定范圍較小、適應性及魯棒性較差及微分信號難于提取等缺陷，應用非線性控制理論，基于非線性跟蹤微分器及PID校正的思想，設計了一種用于靜止無功補償器(SVC)的新型非線性PID控制器。這種控制器具有不依賴于被控系統知識的特點，對系統工作點和網絡結構的變化具有良好的魯棒性且結構簡單，易于實現。數值仿真結果表明，這種非線性PID控制器的控制品質好，不但能有效地改善電力系統功角穩定性和SVC安裝點的電壓動態特性，而且具有較強的適應性和魯棒性。

　　1 引言

　　非線性PID控制器的調節原理為：利用參考輸入和系統輸出的偏差及其微分、積分的非線性組合來產生控制信號，利用非線性特性來改善被控系統的穩態偏差及暫態過程。非線性PID控制器的框圖如圖1，圖中，虛線框部分為非線性PID控制器;v0(t)為系統的參考輸入;u(t)、y(t)分別為系統的控制輸入、輸出; 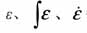分別為偏差、偏差的積分和偏差的微分。

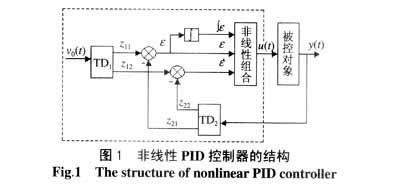
　　跟蹤-微分器[4, 5]TD1用于給出v0(t)理想的過渡過程z11(t)，并給出理想的過渡過程微分信號z12(t)，其中的參數根據過渡過程的快慢要求而定;跟蹤-微分器TD2主要盡快復原y(t)并給出其近似微分，因此，其中的參數要取足夠大。利用2個跟蹤-微分器，即可解決經典的線性PID控制器中微分信號不易提取的問題。

　　基本要素的非線性組合是為了解決線性組合帶來的超調和快速之間的矛盾。確定非線性組合的一個基本標準是：和線性組合相比，偏差小時，采用較大控制;偏差大時，采用較小控制。

　　非線性PID控制器的參數只取決于對象的結構。某一特定對象調好了，按照一定的目標或原則，就能找出適應性、魯棒性很好的一組參數[5, 6]。

　　3 SVC非線性PID控制器的設計

　　3.1 數學模型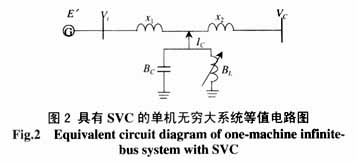

　　具有SVC的單機無窮大系統等值電路圖如圖2所示。假設發電機采用經典二階模型，恒定。其數學模型為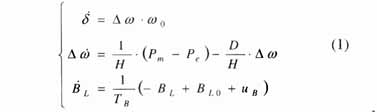

　　式中 d為發電機轉子搖擺角;Dw為發電機轉子角速度增量;w0為系統同步角速度;D為發電機阻尼系數;H為發電機組轉子的慣性時間常數;Pm為發電機機械功率;uB為SVC控制的輸入;TB為SVC及調節系統的慣性時間常數;BL為SVC中可調電感等效電納值;BL0為SVC中可調電感初始電納值;Pe為發電機輸出的電磁功率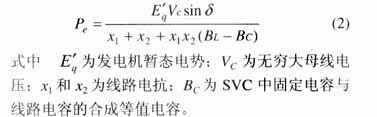

　　3.2 用于SVC的非線性PID控制器的設計

　　將式(1)改寫成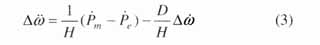

　　式(7)所示為一平滑仿射非線性系統，通過一定的坐標變換，采用反饋線性化方法使其轉化為線性系統，以利于控制器的設計。采用微分幾何理論或直接線性化方法可選取最終坐標變換為

　　將式(8)、(9)代入式(10)，得到SVC的非線性反饋補償規律為

　　式中 z1、z2、z3為反饋線性化模型的狀態變量，v為模型的虛擬控制變量。

　　虛擬控制量v應針對反饋線性化后的標準型設計，理論上已證明，反饋線性化后的系統與原系統具有相同的能控性。可以看出，無論發電機的工作點如何變化，式(11)在形式上是不變的，從而保證了非線性PID型SVC控制器對系統工作點的變化具有較好的魯棒性。另一方面，為了使控制器對于系統網絡結構的變化具有較強的魯棒性，在式(13)中選取z2即發電機角速度誤差變量Δω為反饋變量，構成動態反饋補償，則變換后的發電機角速度誤差變量表達式為

　　式中 δ為決定fal(Δω,α,δ)函數線性區間大小的參數;α為決定該函數的非線性形狀的參數(非線性度)。

　　利用MATLAB仿真工具試算，對比多組不同線性區和非線性度的計算結果，綜合考慮系統指標改善程度和預防系統發生高頻顫振現象的需要，確定a =0.4，d =10-4。

　　為了使發電機達到快速穩定，非線性PID控制的目標必須使發電機功角和角速度盡量同時趨近于穩態值，即兼顧Z1(Δδ/ω0)和z2(Δω)盡快趨近于零，為此，利用MATLAB仿真工具的多次試算進行參數的優化選擇，在上述條件(a, d)下，獲得z1和z2性能較好且系統增益較小的一組PID參數值為：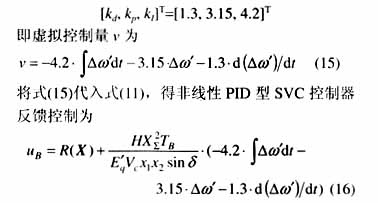

　　4 數值仿真分析

　　仿真系統如圖3所示，發電機及網絡參數為: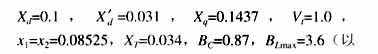

　　上各量的單位均為標幺值)，H=42 s，Td0=10.2s。仿真條件為：系統于t =0.1 s在F點發生三相短路故障, t =0.18 s故障消除, Pe=7.0。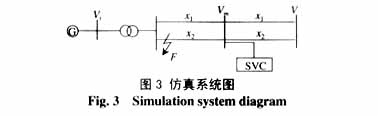

　　圖4給出了系統在常規SVC控制器和非線性PID型SVC控制器作用下的響應曲線，其中, 實線和虛線分別對應在非線性PID型SVC控制器和常規SVC控制器作用下的響應曲線。