|
傳統的機電暫態仿真對HVDC和其它FACTS電力電子裝置采用準穩態模型,因而不能仿真它們的瞬變電壓、電流特性。而電磁暫態仿真程序(例如EMTP)受計算規模的限制,一般要對研究對象的外部電力系統進行等值化簡,因此不能反映系統機電暫態過程對電磁暫態過程的影響。本文介紹的混合仿真算法為彌補上述兩種方法的不足,對電力網絡采用準穩態模型,而對待研究的電力電子裝置(例如SVC)使用電磁暫態模型,兩種仿真的結合使用了本文發展的考慮系統頻率偏移影響的接口技術。本文介紹的混合仿真算法為研究HVDC和FACTS等電力電子裝置及其控制系統的動態性能提供了一種有力的工具。
1 引言
對于等于的雙軸次暫態模型,發電機的等效電路如圖1所示。
當系統未發生擾動,處于穩態運行狀態時,交流系統的頻率保持為基頻。當系統發生大的擾動后,發電機間發生不同程度的搖擺,處于加速機群中的發電機內電勢頻率升高,而處于減速機群中的發電機內電勢頻率降低。由于故障中各發電機內電勢頻率的不一致,導致EMTP子系統中諾頓電流源的頻率難以用系統中各發電機內電勢頻率的顯式函數來表達。因此,本文根據擾動中和擾動后SVC安裝母線電壓頻率偏移,動態地計算SVC母線的瞬時頻率fe作為EMTP諾頓等效電源的頻率,并認為在一次EMTP子程序仿真時,諾頓電流源頻率保持不變。
2.2EMTP對TSP的等效
EMTP仿真得到的是反映SVC接口母線處的電壓、電流瞬時值的離散數據點,因此需要對其進行信號處理以求得TSP仿真需要的數據。常用離散傅立葉變換或最小二乘曲線擬合的方法求取SVC母線電壓、注入網絡電流的基頻分量和各次諧波分量。離散傅立葉變換求取信號的基頻分量需要獲得整周波的數據,而最小二乘曲線擬合方法不受此限制,因此最小二乘曲線擬合方法具有更大的靈活性。
由于TSP仿真基于基頻正序單相相量模型,所以在使用最小二乘曲線擬合方法時只需求取SVC基頻等效負荷,而忽略SVC母線電壓和注入網絡電流的各次諧波分量。未考慮SVC諧波源對外部系統的作用將會給混合仿真帶來一定誤差,但是由于SVC本身具有諧波濾波裝置用以濾除5、7次等特征諧波。同時SVC變壓器二次側采用三角形聯接,在穩態情況下3的倍數次諧波不能流入外部網絡。因此SVC諧波源對混合仿真精度的影響不大。 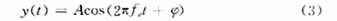
式中,電壓或電流信號頻率fe由式(2)計算。
使用式(3)對EMTP仿真得到的電壓和電流的三相瞬時值分別進行最小二乘曲線擬合,即可求得電壓、電流相量的幅值A和相角φ。根據SVC母線電壓、注入網絡電流相量,即可求出SVC的基頻等效負荷。由于機電暫態系統相對于電磁暫態系統而言屬于慢變系統,因此可以認為SVC的等效負荷在一個TSP積分步長內保持不變。即SVC在一個TSP積分步長內對外部網絡等效為恒功率負荷。
2.3混合仿真的同步和數據交換
由于TSP和EMTP采用的積分時間步長不同,兩種仿真只能在特定的時間點進行數據交換。也就是說,TSP仿真一步,EMTP仿真多步,并在TSP的各時間點進行數據交換。混合仿真計算過程如圖2所示。
步驟如下:
(1)計算潮流,求取T0時刻TSP子系統的仿真初值;
(2)求取TSP對EMTP的諾頓等效電路和接口母線瞬時頻率(箭頭1);
(3)在T0至T1時刻之間進行EMTP仿真,求取SVC的電壓、電流瞬時值(箭頭2);
(4)對EMTP仿真得到的接口母線處電壓、電流三相瞬時值進行曲線擬合,求取基頻正序分量,EMTP對TSP等效為負荷(箭頭3);
(5)在T0至T1時刻之間進行TSP仿真,求取T1時刻TSP仿真變量(箭頭4);
(6)如果網絡結構突變,修改節點導納矩陣,求取TSP子系統擾動后的仿真初值;
|